Question

It’s been a while since I did Math but, in most scenarios, when you solve for an equation with only 1 x variable and you substitute it back in, it should always be true and equal the answer in the original equation(?).

For this equation, the answer was x=7, but when I substitute it back in, I was unable to get the original solution back, which means it is “no solution” after all.
Why is that?

Answer 1

Let's replace every copy of x with 7 and simplify.

`√(5x+1)+9 = 3\\\\√(5*7+1)+9 = 3\\\\√(35+1)+9 = 3\\\\√(36)+9 = 3\\\\6+9 = 3 \ \text{ .... note the 6 on the left isn't negative}\\\\15 = 3\\\\`

Which is clearly false. This is probably the set of steps you followed to get "no solution".

Why is there no solution? Well let's subtract 9 from both sides to isolate the square root

`√(5x+1)+9 = 3\\\\√(5x+1)+9-9 = 3-9\\\\√(5x+1) = -6\\\\`

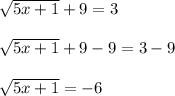
Recall that the result of a square root operation is never negative. The range of
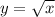`y = √(x)` and
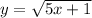`y = √(5x+1)` is the set of nonnegative numbers. There is no way we can have the left hand side result in -6

If there was a negative sign out front the square root and we have this instead

`-√(5x+1)+9 = 3\\\\`

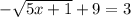
then the answer would be x = 7

Unfortunately, there isn't such a negative sign, so we stick with "no solutions".