Check the picture below.
so hmmm if Lydia is correct, then there's one angle in the triangle that is 90°, hmmm well, looking at the picture, we can pretty much forget about angle Z or Y, they're both acute, hmm how about angle X? is it 90°?
well, if angle X is indeed a right-angle, the lines XZ and XY are perpendicular, but are they? if that's so then the slopes of XZ and XY are negative reciprocal of each other, let's check
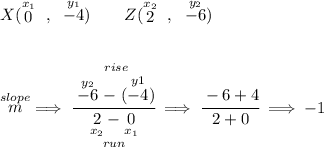
now, the negative reciprocal of that will be
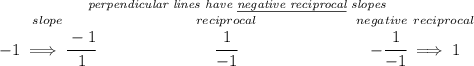
well, let's see if XY has a slope is 1 then
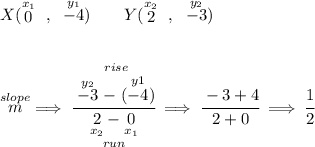
OMG!!! Lydia needs to go get a nice Latte with cinnamon and to recheck her triangle.