Answer:
In a nutshell,
 cannot be 3 or 6 in the inverse function for all
cannot be 3 or 6 in the inverse function for all
 distinct from 2 and 5.
distinct from 2 and 5.
Explanation:
From Functional Theory we remember that a function is a relation in which all elements of its domain has an unique and different element from range. If
 is the image of the inverse, which is a function, then
is the image of the inverse, which is a function, then
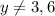 . Otherwise, the inverse could not be a function when
. Otherwise, the inverse could not be a function when
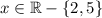 .
.
In a nutshell,
 cannot be 3 or 6 in the inverse function for all
cannot be 3 or 6 in the inverse function for all
 distinct from 2 and 5.
distinct from 2 and 5.