Question

The table shows the viscosity of an oil as a function of temperature. Identify a quadratic model for the viscosity, given the temperature. Then use the model to predict the viscosity of the oil at a temperature of 140°C.

Answer 1

f(x) ≈ 0.001x2 − 0.37x + 39.4

The viscosity of the oil at 140°C is about 7.2 kg/ms.

Explanation:

Substitute the values of a, b, and c into f(x) = ax2 + bx + c to write the quadratic model.

f(x) ≈ 0.001x2 − 0.37x + 39.4

Evaluate the quadratic model for x = 140 and simplify to predict the viscosity of the oil at a temperature of 140°C.

f(140) ≈ 0.001(140)2 − 0.37(140) + 39.4 ≈ 7.2

Therefore, the viscosity of the oil at a temperature of 140°C is about 7.2 kg/ms.

Answer 2

The viscosity at 140°C is predicted to be 7.2

Explanation:

The function that model the relationship between viscosity and temperature = Quadratic model

The general form of a quadratic equation is y = a·x² + b·x + c

Therefore, we have;

When y = 10.8, x = 110, which gives;

10.8 = a·110² + b·110 + c = 12100·a + 110·b + c

10.8 = 12100·a + 110·b + c

When y =8.2, x = 130

8.2 = a· 130² + b· 130 + c = 16900·a + 130·b + c

8.2 = 16900·a + 130·b + c

When y = 160, x = 5.8

5.8 = a·160² + b·160 + c = 25600·a + 160·b + c

5.8 = 25600·a + 160·b + c

The three equations above can be listed as follows;

10.8 = 12100·a + 110·b + c

8.2 = 16900·a + 130·b + c

5.8 = 25600·a + 160·b + c

Solving using matrices gives;

`\begin{bmatrix}12100 & 110 & 1\\ 16900 & 130 & 1\\ 25600 & 160 & 1\end{bmatrix} \begin{bmatrix}a\\ b\\ c\end{bmatrix} = \begin{bmatrix}10.8\\ 8.2\\ 5.8\end{bmatrix}`

`\begin{bmatrix}a\\ b\\ c\end{bmatrix} = -(1)/(3000)\begin{bmatrix}3 & -5 & 2\\ -867 & 1350 & -480\\ 62400 & -88000 & 28600\end{vmatrix} \begin{bmatrix}10.8\\ 8.2\\ 5.8\end{bmatrix}`

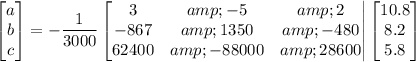
From which we have;

a = 0.001, b = -0.37, c = 39.4

Substituting gives;

y = 0.001·x² - 0.37·x + 39.4

When x = 140

y = 0.962·140² - 0.37·140 + 39.4= 7.2

The viscosity at 140°C = 7.2.