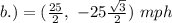Question

A hand glider dives at 25 mph in a direction 60° below

horizontal. What is the component form of the velocity vector?

a. (25-2, 25squareroot3/2)
b. (25/2, -25squareroot3/2)
c. (-25/2, 25squareroot3/2)
d. (-25/2, -25squareroot3/2)

Answer 1

B: (25/2, - 25√3/2)

Explanation:

First find the values

v = 25 mph

θ = 60°

Vertical:

`V_(y)` = -vsin(θ) (Negative because it is below the x axis.)

`V_(y)` = (-25)(sin(60))

`V_(x)` = (-25)(
`(√(3) )/(2)`)

`V_(y)` =
`(-25√(3) )/(2)`

Horizontal:

`V_(x)` = vcos(θ)

`V_(x)` = (25)(cos(60))

`V_(x)` = (25)(1/2)

`V_(x)` =
`(25)/(2)`

Putting them together we get:

(
`(25)/(2)`,
`(-25√(3) )/(2)`) or B

Answer 2

`b.)= ((25)/(2) , \ -25(√(3) )/(2))\ mph`

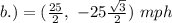
Explanation:

Given;

velocity of the diver, v = 25 mph

direction of his dive, θ = 60°

The vertical component of the velocity is given by;

`-V_y = vsin\theta \ \ (below \ horizontal \ is \ in \ negative\ y-direction)\\\\V_y =-(25)(sin 60)\\\\V_y =-(25)((√(3) )/(2) )`

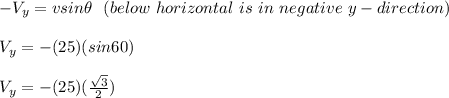
The horizontal component of the velocity is given by;

`V_x =vcos\theta\\\\V_x =(25)(cos 60 )\\\\V_x =(25)((1 )/(2) )\\\\V_x = (25)/(2)`

Therefore, the component form of the velocity vector is given by;

`(V_x, \ V_y) = ((25)/(2) , \ -25(√(3) )/(2))\ mph`

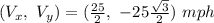
correct option =
`b.)= ((25)/(2) , \ -25(√(3) )/(2))\ mph`