Question

What is the slope of the line that passes through the points (-6, 8) and (-9, 7)? Write your answer in simplest form.

Answer 1

m=1/3

equation y=1/3x+10

Explanation:

Find the rise and run.

1. -6--9=run=3

2. 8-7=rise=1

Answer 2

Hi student, let me help you out! :)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

We are asked to find the slope of the line that passes through (-6, 8) and (-9, 7).

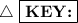`\triangle~\fbox{\bf{KEY:}}` (formula for Slope)

`\longmapsto\bf{\cfrac{y2-y1}{x2-x1}}`

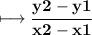
y2 & y1 = the y-coordinates of the two points

x2 & x1 = the x-coordinates of the two points

`\ddot\bigstar` Remember this...

`\fbox{y2\;and\;y1\;are\;y-coordinates\;of\;the\;two\;points,\;and\;x2\;and\;x1\;are\;x-coordinates}}`

So we substitute the values and obtain:

`\bf{\cfrac{7-8}{-9-(-6)}`

Simplifying:

`\bf{\cfrac{-1}{-9+6}}`

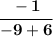
Simplifying more:

`\bf{\cfrac{-1}{-3}}`

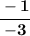
Divide the top and bottom by -1:

`\bf{\cfrac{1}{3}}`

There's the slope.

Hope it helps you out! :D

Ask in comments if any queries arise.

~Just a smiley person helping fellow students