Question

Bridgette has $1,000 to invest. She has two different investment options, shown in the table below. Each option would give her a different value over three years.

Number of Years 1 2 3
Option A (amount in dollars) 1100 1200 1300
Option B (amount in dollars) 1100 1210 1331


Part A: What type of function, linear or exponential, would be best to describe the value of the investment over a fixed number of years using Option A? Explain your answer.

Part B: Write a function, a(t), to describe the value of the investment, in dollars, of Option A after t years.

Part C: What type of function, linear or exponential, would be best to describe the value of the investment over a fixed number of years using Option B? Explain your answer.

Part D: Write a function, b(t), to describe the value of the investment, in dollars, of Option B after t years.

Part E: Bridgette wants to invest in whichever option would increase her investment value by the greatest amount in 20 years. Will there be any significant difference in the value of Bridgette's investment after 20 years if she uses Option A over Option B? Explain your answer, and show the investment value after 20 years for each option.

Answer 1

Part A:

Option A is a linear function

Part B:

a(t) = t × 100 + 1000

Part C:

Option B is an exponential function

Part D

`b(t) = 1000 * (1 + 0.1)^t`

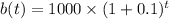
Part E:

There will be a significant difference in the value of Bridget's investment after 20 yeas if she uses Option A over Option B

Explanation:

The given parameters are;

The amount Bridgette has to invest = $1,000

The value of each investment option is given as follows;

Number of years
`{}` Option A
`{}` Option B

1
`{}` 1100 1100

2
`{}` 1200 1210

3
`{}` 1300 1331

Part A:

Given that the first difference between subsequent data values are 2 - 1 = 1 and 1200 - 1100 = 100, 3 - 2 = 1 and 1300 - 1200 = 100 both of which are constant, the type of function that would be best to describe option A is a linear function

Part B:

The function a(t) for Option A is given as follows;

The rate of change of the function amount with time is (1300 - 1200)/(3 - 2) = 100

Therefore, comparing with the general form of a linear function, y = m·x + c, we have;

m = The rate of change of the function = 100

The y-intercept, the value of the amount a 0 time (the start of the investment) = c = 1000

The function in terms of t, a(t) = t × 100 + 1000

Part C:

The first difference of Option B are different but the first ratio given as follows;

1210/1100 = 1331/1210 = 1.1 = Constant which is the characteristics of an exponential variable

Therefore, the equation to describe the value of the investment in dollars, of Option B is an exponential function

Part D

We, have for an exponential function;

`b(t) = 1000 * (1 + r)^t`

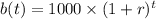
When t = 1, we have;

`b(1) = 1000 * (1 + r)^1 = 1100`

∴ 1 + r = 1100/1000 = 1.1

r = 1.1 - 1 = 0.1

We check for t = 2, to get;

`a(2) = 1000 * (1 + 0.1)^2 = 1210`

We check for t = 3, to get;

`b(3) = 1000 * (1 + 0.1)^3 = 1331`

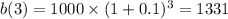
The function b(t) to describe the value of the investment in dollars, of Option B after t years is
`b(t) = 1000 * (1 + 0.1)^t`

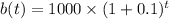
Part E:

The investment value after 20 years is given as follows;

For Option A, we have;

a(20) = 20 × 100 + 1000 = 3000

For Option B, we have;

`b(20) = 1000 * (1 + 0.1)^(20) \approx 6727.5`

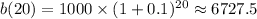
Therefore, the difference in the investment value after 20 years for Option B and Option A is approximately $6727.5 - $3000 = $3727.5 which is significant.