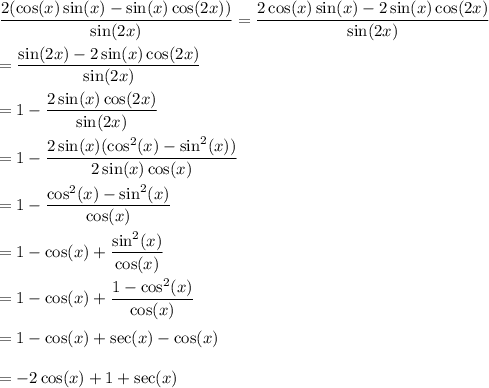This is not an identity.
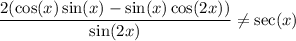
Check x = π/4, for which we have cos(π/4) = sin(π/4) = 1/√2. Together with sin(2•π/4) = sin(π/2) = 1 and cos(2•π/4) = cos(π/2) = 0, the left side becomes 1, while sec(π/4) = 1/cos(π/4) = √2.
Keeping the left side unchanged, the correct identity would be
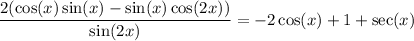
To show this, recall
• sin(2x) = 2 sin(x) cos(x)
• cos(2x) = cos²(x) - sin²(x)
• cos²(x) + sin²(x) = 1
Then we have