Question

Slopes of parallel \perpendicular lines

Answer 1

Hello, the answer should be
`m=(6)/(5)= 1,2`.

First, let's edit the given function as
`y` parameter leave alone.

`15x+18y=270\\\\18y=270-15x\\\\y=(270-15x)/(18)\\ \\y=(270)/(18)-(15x)/(18)`

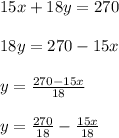
IMPORTANT!

If the given equation looks like;

`y=f(x)\\\\y=ax+b`

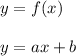
then, the slope of the equation is the coefficient of
`x` parameter (
`a`)

The slope(m);

`m=(-15)/(18)=(-5)/(6)`

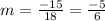
The product of the slopes of two perpendicular lines must be
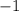`-1`. By that way, the slope of a line perpendicular to the given line is below:

`m_(expected)=(-1)/(m_(given)) \\\\m_(expected)=(-1)/((-5)/(6) )=(6)/(5)`

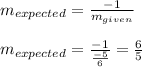
Good luck. If you have any questions, then feel free to ask in comments!