Question

Finding the slope from points

Answer 1

m = -3

Explanation:

Given two points:

• (-1,-7) & (1,-13)

To Find:

• The slope

Solution:

Using slope's formulae,

• [m denotes slope]

`\boxed{ \rm{m = \cfrac{y_2 -y_1 }{x_2 - x_1} }}`

According to the question, on the formula:

• (y_2,y_1) = (-13,-7)
• (x_2,x_1) = (1,-1)

Substitute them onto the formulae:

`\rm \: m = \cfrac{ - 13 - ( - 7)}{1 - ( - 1)}`

Simplify using PEMDAS:

• P = Parentheses
• E = exponents
• M = Multiplication
• D = Division
• A = addition
• S = subtraction

`\rm \: m = \cfrac{ - 13 + 7}{1 \ + 1}`

`\rm \: m = \cfrac{ - \cancel6}{ \cancel2} = \boxed{ - 3}`

Hence, the slope of the line that passes through the given points in it's simplest form is -3.

Answer 2

m = -3

Explanation:

The formula to find the slope of the line is :

slope = m =
`(y_1 - y_2)/(x_1-x_2)`

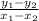
Given that the two coordinates of the line are :

( -1 , - 7 ) ⇒ ( x₁ , y₁ )

( 1 , -13 ) ⇒ ( x₂ , y₂ )

Let us solve now.

m = ( y₁ - y₂ ) ÷ ( x₁ - x₂ )

m = ( -7 - ( -13)) ÷ ( -1 - 1 )

m = ( -7 + 13 ) ÷ ( -2 )

m = 6 ÷ -2

m = -3