Given:
The edge length of a cube is changing at a rate of 10 in/sec.
To find:
The rate by which cube's volume changing when the edge length is 3 inches.
Solution:
We have,
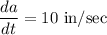
We know that, volume of cube is
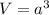
Differentiate with respect to t.
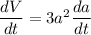
Substituting
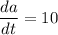 and a=3, we get
and a=3, we get

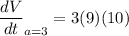

Therefore, the volume increased by 270 cubic inches per sec.