Question

The edge length of a cube is changing at a rate of 10 in/sec. At what rate is the cube's volume changing when the edge length is 3 inches?

Answer 1

Given:

The edge length of a cube is changing at a rate of 10 in/sec.

To find:

The rate by which cube's volume changing when the edge length is 3 inches.

Solution:

We have,

`(da)/(dt)=10\text{ in/sec}`

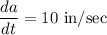
We know that, volume of cube is

`V=a^3`

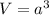
Differentiate with respect to t.

`(dV)/(dt)=3a^2(da)/(dt)`

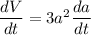
Substituting
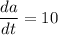`(da)/(dt)=10` and a=3, we get

`(dV)/(dt)_(a=3)=3(3)^2(10)`

`(dV)/(dt)_(a=3)=3(9)(10)`

`(dV)/(dt)_(a=3)=270`

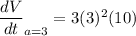
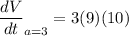
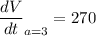
Therefore, the volume increased by 270 cubic inches per sec.