Answer:
The value is

Step-by-step explanation:
From the question we are told that
The velocity of the electron is
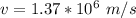
The mass of the electron is
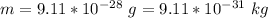
Generally the deBroglie wavelength is mathematically represented as
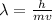
Here h is the Planck'c constant with value
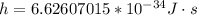
So
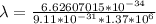
=>
