Answer:
(a) 0.7472
(b) 0.2397
(c) 3.6
Explanation:
Let X denote the number of children who are hyperlipidemic.
The proportion of children who are hyperlipidemic is, p = 0.30.
A random sample of n = 12 children are analyzed.
Every child is independent of the others to be expected to meet the criteria for hyperlipidemia.
The random variable X follows a binomial distribution with parameters n = 12 and p = 0.30.
(a)
Compute the probability that at least 3 are hyperlipidemic as follows:
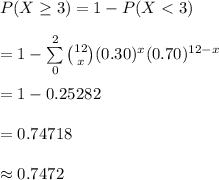
Thus, the probability that at least 3 are hyperlipidemic is 0.7472.
(b)
Compute the probability that exactly 3 are hyperlipidemic as follows:

Thus, the probability that exactly 3 are hyperlipidemic is 0.2397.
(c)
Compute the expected number of children who would meet the criteria for hyperlipidemia as follows:
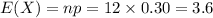
Thus, 3.6 children would be expected to meet the criteria for hyperlipidemia.