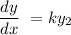Answer:
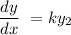
Explanation:
The rate of change of y with respect to x is expressed as shown;
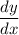
If the rate of change of y with respect to x is proportional to y2, this is expressed as;
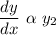
If we remove the proportionality sign, a proportionality constant will be introduced as shown;
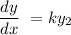
where k is the constant of proportionality.
Hence the differential equation for the statement is expressed as