Question

Find the complex power, average power, and reactive power for the following:

v(t) = 339.4 sin (377t + 90°) V, i(t) = 5.657 sin (377t + 60°) A

Answer 1

Step-by-step explanation:

Given that:

v(t) = 339.4 sin(377t + 90°) V

i(t) = 5.657 sin (377t + 60°) A

v = 339.4 ∠ 90°
`v_m \angle\phi_1`

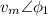
i = 5.657∠60°
`I_m \angle \phi_2`

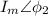
The phase difference
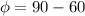`\phi = 90 -60` = 30

The average power
`P_(avg)` can be expressed as:

`P_(avg) = (v_m)/(√(2))(I_m)/(√(2)) * cos (30)`

`P_(avg) = (339.4)/(√(2))*(5.657)/(√(2)) * cos (30)`

`\mathbf{P_(avg) = 831.38 \ watts}`

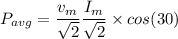
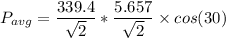
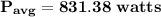
The reactive power Q is as follow;

`Q = (v_m)/(√(2)) * (I_m)/(√(2)) \ sin \phi\\`

`Q = (339.4)/(√(2))*(5.657)/(√(2)) * sin (30)`

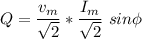
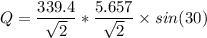
Q = 479.99 VAR

The complex power S = P + jQ

The complex power S = 831.38 W + j479.99 VAR