Answer:
Ф =
![(Q)/(e_(0) ) [ ((4\pi )/(3 )(R)^3 )/((4)/(3)\pi (R)^3 ) ]](https://img.qammunity.org/2021/formulas/engineering/college/o0n6jwtusg8a42xd2wxv8o79xq327zsvrk.png)
Step-by-step explanation:
Radius of Gaussian surface = R
Charge in the Sphere ( Gaussian surface ) = Q
lets take the radius of the sphere to be equal to radius of the Gaussian surface i.e. R
To determine the net electric flux through the Gaussian surface
we have to apply Gauci law
Ф = 4

Ф =
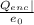
=
![(Q)/(e_(0) ) [ ((4\pi )/(3 )(R)^3 )/((4)/(3)\pi (R)^3 ) ]](https://img.qammunity.org/2021/formulas/engineering/college/o0n6jwtusg8a42xd2wxv8o79xq327zsvrk.png)