Question

A bus initially moving at 20 m/s with an acceleration of -4m/s² for 5

seconds. What is the displacement AND final velocity?

Answer 1

50m; 0m/s.

Step-by-step explanation:

Given the following data;

Initial velocity = 20m/s

Acceleration, a = - 4m/s²

Time, t = 5secs

To find the displacement, we would use the second equation of motion;

`S = ut + \frac {1}{2}at^(2)`

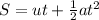
Substituting into the equation, we have;

`S =20*5 + (1)/(2)*(-4)*5^(2)`

`S =100 + (-2)*25`

`S =100 - 50`

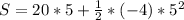
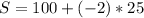
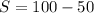
S = 50m

Next, to find the final velocity, we would use the third equation of motion;

`V^(2) = U^(2) + 2aS`

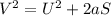
Where;

• V represents the final velocity measured in meter per seconds.

• U represents the initial velocity measured in meter per seconds.

• a represents acceleration measured in meters per seconds square.

Substituting into the equation, we have;

`V^(2) = 20^(2) + 2(-4)*50`

`V^(2) = 400 - 400`

`V^(2) = 0`

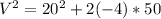
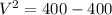
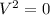
V = 0m/s

Therefore, the displacement of the bus is 50m and its final velocity is 0m/s.