Question

A certain model of remote-control Stanley garage door opener has nine binary (off/on) switches. The homeowner can set any code sequence. (a) How many separate codes can be programmed

Answer 1

`Codes= 512`

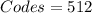
Explanation:

Given

`Switches = 9`

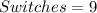
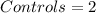`Controls = 2` ------- on or off

Required

Determine the number of codes to be programmed

Since each switch has any of the on or off controls (i.e on or off), then:

The first switch can be coded in any of the 2 controls

The second switch can be coded in any of the 2 controls

The third switch can be coded in any of the 2 controls

Up till the ninth switch

So, we have that:

`Codes= 2 * 2 *2*2*2* 2 *2*2*2`

`Codes = 2^9`

`Codes= 512`

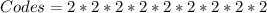
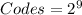
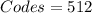
Hence, there are 512 possible codes