Question

How long will it take an investment to double in value if the interest rate is 6% compounded continuously

Answer 1

11.55 years

Explanation:

Formula to calculate the final value when the money is compounded continuously is,

Final value =
`\text{(Present value)}.e^(rt)`

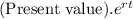
Here 'r' = rate of interest

t = duration for the investment

Let the money invested = $x

We have to find the duration in which the present value gets doubled.

Final value = $2x

Rate of interest = 6% per year ≈ 0.06

By substituting these values in the formula,

`2x=x.e^(0.06t)`

`2=e^(0.06t)`

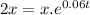
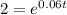
ln(2) =
`\text{ln}e^(0.06t)`

0.693147 = 0.06t

t = 11.55 years

Therefore, invested amount will be doubled in 11.55 years.