Question

11) Which of the following is zero of the polynomial x^3+x^2+x+1

1
-1
both options 1 and 2
None
please answer​

Answer 1

Answer: -1

Explanation:

The Polynomial Remainder Theorem

It states that the remainder of the division of a polynomial f(x) by (x-r) is equal to f(r).

We have the polynomial:

`f(x)=x^3+x^2+x+1`

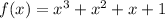
And we need to determine if x=1 and/or x=-1 are zeros of the polynomial.

Considering the polynomial remainder theorem, if we try any value for x, and the remainder is zero, then that value of x is a root or zero of the polynomial.

Find:

`f(1)=1^3+1^2+1+1`

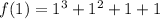
f(1)=4

Thus, x=1 is not a zero of f(x)

Now, find:

`f(-1)=(-1)^3+(-1)^2+(-1)+1`

`f(1)=-1+1-1+1=0`

Thus, x=-1 is a zero of f(x)

Answer: -1