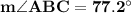Question

BD bisects m m Find m

Answer 1

The text of the question is not visible in the answering window. I'll reproduce it here:

BD bisects <ABC.

m <ABD= 2.5x + 8.6

m<CBD = 3.5x - 3.4

Find m<ABC

Answer:

`m\angle ABC = 77.2^\circ`

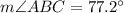
Explanation:

We have an angle ABC and a line BD bisecting it.

If an angle is bisected, then the two formed angles are congruent, that is

`m\angle ABD=m\angle CBD`

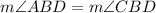
Substituting the algebraic expressions for both angles:

`2.5x + 8.6=3.5x - 3.4`

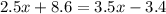
Subtracting 8.6 and 3.5x:

`2.5x - 3.5x = -8.6 - 3.4`

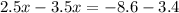
Operating:

`-x = -12`

`x = 12`

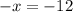
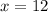
The two angles are:

`m\angle ABD=2.5x + 8.6=2.5(12) + 8.6=38.6^\circ`

`m\angle CBD=3.5x - 3.4 = 38.6^\circ`

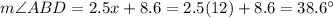
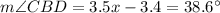
As expected, both angles have the same measure.

The measure of the total angle ABC is twice any of those:

`m\angle ABC = 2*38.6^\circ=77.2^\circ`

`\mathbf{m\angle ABC = 77.2^\circ}`