Answer:
case a) y=1/3x+8
case b) y=-3x+28
Explanation:
case a)
parallel lines has the same slope, then, the searched line has the form:
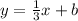
Now, in order to find b, we must use the given point (6,10). By substituying this point into the last equation, one has
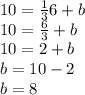
Then, the line equation is y=1/3x+8
case b)
the slope of a perpendicular line is the "negative reciprocal" of the slope of the original line, that is

Hence, the searched line has the form y=-3x + b. Now, in order to find the y-intercept b, we must use the given point (6,10). Therefore,

Hence, the searced equation is y=-3x+28