Question

A company sells 14 types of crackers that they label varieties 1 through 14, based on spice level. What is the probability that the purchase results in a selection of a cracker with an odd number, or a number greater than 11?

Answer 1

The required probability is
`\mathit{(9)/(14)}`

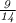
Explanation:

Probability: Rule of Addition

The probability that Event A or Event B occurs is equal to the probability that Event A occurs plus the probability that Event B occurs minus the probability that both Events A and B occur. It can be calculated as follows:

P(A ∪ B) = P(A) + P(B) - P(A ∩ B)

There are 14 types of crackers the company sells, numbered from 1 to 14. The sample space for purchasing one cracker is:

`\Omega=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14\}`

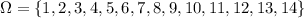
There are n=14 possible choices.

The favorable cases for a cracker with an odd number are:

A = {1,3,5,7,9,11,13}

There are 7 favorable cases.

The favorable cases for a cracker with a number greater than 11 are:

B = {12,13,14}

There are 3 favorable cases.

The cases which are common to both events are:

A ∩ B= {13}

There is 1 case.

The probability of each event is:

`\displaystyle P(A)=(7)/(14)=(1)/(2)`

`\displaystyle P(B)=(3)/(14)`

`\displaystyle P(A\cap B)=(1)/(14)`

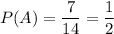
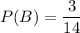
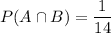
Therefore:

`\displaystyle P(A\cup B)=(1)/(2)+(3)/(14)-(1)/(14)`

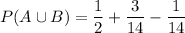
Adding the fractions:

`\displaystyle P(A\cup B)=(7+3-1)/(14)=(9)/(14)`

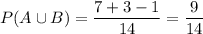
The required probability is
`\mathbf{(9)/(14)}`