Question

Find the equation of the line L which is perpendicular to the line 3x - 2y + 6 = 0 and passes through the point (3, -5)

Answer 1

keeping in mind that perpendicular lines have negative reciprocal slopes, let's check for the slope of the equation above

`3x-2y+6=0\implies 3x-2y=-6\implies -2y=-3x-6 \implies y=\cfrac{-3x-6}{-2} \\\\\\ y=\cfrac{-3x}{-2}-\cfrac{6}{-2}\implies y=\stackrel{\stackrel{\stackrel{m}{\downarrow }}{}}{\cfrac{3}{2}} x+3\qquad \impliedby \begin{array}ll \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}`

therefore then

`\stackrel{\textit{perpendicular lines have \underline{negative reciprocal} slopes}} {\stackrel{slope}{\cfrac{3}{2}} ~\hfill \stackrel{reciprocal}{\cfrac{2}{3}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{2}{3}}}`

so we're really looking for the equation of a line whose slope is -2/3 and passes through (3 , -5)

`(\stackrel{x_1}{3}~,~\stackrel{y_1}{-5})\qquad \qquad \stackrel{slope}{m}\implies -\cfrac{2}{3} \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-5)}=\stackrel{m}{-\cfrac{2}{3}}(x-\stackrel{x_1}{3}) \\\\\\ y+5=-\cfrac{2}{3}x+2\implies y=-\cfrac{2}{3}x-3`

Answer 2

`\displaystyle y = -(2)/(3)\, x - 3`.

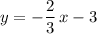Explanation:

Rewrite the equation
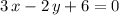`3\, x - 2\, y + 6 = 0` in the slope-intercept form
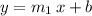`y = m_(1) \, x + b` to find the slope of this given line:

`\displaystyle y = (3)/(2)\, x + 3`.

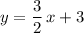Thus, the slope of this given line is
`m_(1) = (3/2)`.

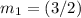Let
`m_(1)` and
`m_(2)` denote the slope of the given line and the slope of line
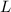`L`, respectively. Two lines in a plane are perpendicular to one another if and only if the product of their slopes is
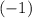`(-1)`. Therefore, for these two lines to be perpendicular to one another,
`m_(1) \, m_(2) = (-1)`.

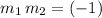Since
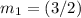`m_(1) = (3/2)` according to the equation of the given line, the slope of line
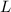`L` would be:

`\begin{aligned} m_(2) &= ((-1))/(m_(1)) \\ &= ((-1))/((3/2)) \\ &= ((-2))/(3)\end{aligned}`.

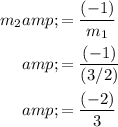If a line in a plane has slope
`m` and goes through the point
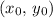`(x_(0),\, y_(0))`, the slope-point equation of that line would be
`(y - y_(0)) = m\, (x - x_(0))`.

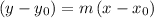Since the line
`L` goes through
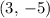`(3,\, -5)`, the equation of this line in slope-point form would be:

`\displaystyle y - (-5) = ((-2))/(3)\, (x - 3)`.

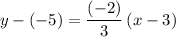Rearrange to find the equation of line
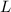`L` in slope-intercept form:

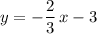`\displaystyle y = -(2)/(3)\, x - 3`.