Answer: B. 5/13
This is the same as writing

==========================================================
Reason:
We have two given sides of this right triangle. Use the pythagorean theorem to find the missing side.
a = 5 and b = 12 are the two known legs; c is the unknown hypotenuse
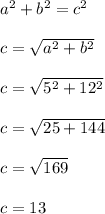
The hypotenuse is exactly 13 units long. This is a 5-12-13 right triangle.
Now we can compute sine of theta
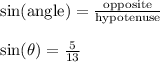
This points us to choice B as the final answer.
----------------
Extra Info (optional)
- 5/12 is the value of tan(theta) since it's opposite/adjacent
- 12/5 is the value of cot(theta), the reciprocal of tangent
- 12/13 is the value of cos(theta), because cos = adjacent/hypotenuse