Statement :- We assume the orthagonal sequence
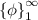 in Hilbert space, now
in Hilbert space, now
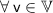 , the Fourier coefficients are given by:
, the Fourier coefficients are given by:
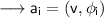
Then Bessel's inequality give us:
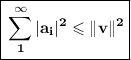
Proof :- We assume the following equation is true
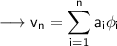
So that,
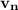 is projection of
is projection of
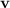 onto the surface by the first
onto the surface by the first
 of the
of the
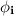 . For any event,
. For any event,
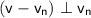
Now, by Pythagoras theorem:
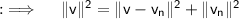
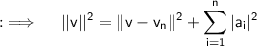
Now, we can deduce that from the above equation that;
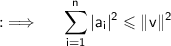
For
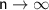 , we have
, we have
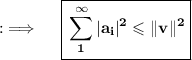
Hence, Proved