Question

State and prove bessel inequality​

Answer 1

hope this helps and if you have any questions please feel free to ask me any time

Answer 2

Statement :- We assume the orthagonal sequence
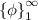`{{\{\phi\}}_(1)^(\infty)}` in Hilbert space, now
`{\forall \sf \:v\in \mathbb{V}}`, the Fourier coefficients are given by:

`{\quad \qquad \longrightarrow \sf a_(i)=(v,{\phi}_(i))}`

Then Bessel's inequality give us:

`{\boxed{\displaystyle \bf \sum_(1)^(\infty)\vert a_(i)\vert^(2)\leqslant \Vert v\Vert^(2)}}`

Proof :- We assume the following equation is true

`{\quad \qquad \longrightarrow \displaystyle \sf v_(n)=\sum_(i=1)^(n)a_(i){\phi}_(i)}`

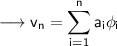
So that,
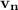`{\bf v_n}` is projection of
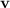`{\bf v}` onto the surface by the first
`{\bf n}` of the
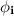`{\bf \phi_(i)}` . For any event,
`{\sf (v-v_(n))\perp v_(n)}`

Now, by Pythagoras theorem:

`{:\implies \quad \sf \Vert v\Vert^(2)=\Vert v-v_(n)\Vert^(2)+\Vert v_(n)\Vert^(2)}`

`^(2)=\Vert v-v_(n)\Vert^(2)+\sum_(i=1)^(n)\vert a_(i)\vert^(2)`

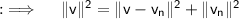
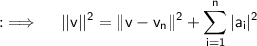
Now, we can deduce that from the above equation that;

`{:\implies \quad \displaystyle \sf \sum_(i=1)^(n)\vert a_(i) \vert^(2)\leqslant \Vert v\Vert^(2)}`

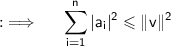
For
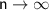`{\sf n\to \infty}`, we have

`{:\implies \quad \boxed{\displaystyle \bf \sum_(1)^(\infty)\vert a_(i)\vert^(2)\leqslant \Vert v\Vert^(2)}}`

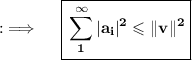
Hence, Proved