Answer:
C. j=2 and h=4
Explanation:
Step 1: Create a system of equations for your problem based off what we know.
- we should know that the equation to find the perimeter of something is
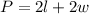 where P is the perimeter, l is the length, and w is the width.
where P is the perimeter, l is the length, and w is the width.
- we know that the perimeter of Rectangle P is 20 inches and that the perimeter of Rectangle Q is 30
- we know the length and width of both rectangles
Using this information, lets set up our system.:
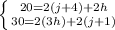
Step 2: Using the top equation we're going to try to solve for one of the variables. I chose to solve for variable j.
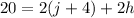
Start by distributing 2 into j + 4.
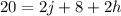
Now subtract 8 from both sides of the equation.
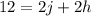
Now isolate variable j by subtracting 2h from both sides of the equation.
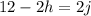
Now condense the equation into simple terms by dividing both sides by its GCF 2 then reorder to get j on the left.
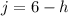
Step 3: Now that we solved for variable j we can now substitute j into one of our equations from the original system. I chose to use the bottom equation and chose to distribute it before substituting.
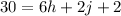
Subtract two from both sides to isolate the variables
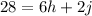
Now we can plug j into our equation
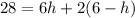
Step 4: Distribute 2 into 6-h
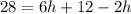
Step 5: Combine like terms
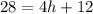
Step 6: Subtract 12 from both sides of the equation

Step 7: Divide both sides by 4
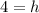
Now that we know that h=4 we can plug 4 into one of our earlier equations. I used j=6-h
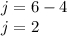
Plug answers into either one of the original equations to check answer