Answer: 0.2224
Explanation:
Given: The proportion of adults need eye correction: p= 78%=0.78
Let X be a binomial variable that represents the number of adults who need eye correction.
Sample size of adults: n= 12
Binomial ditsribution formula:
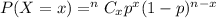
Now, the probability that at least 11 of them need correction for their eyesight will be
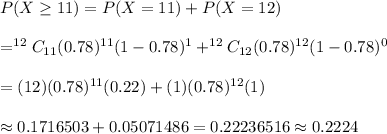
Hence, the required probability = 0.2224