Consider the linear system: \overrightarrow y'=\begin{bmatrix}-6 & -4 \\12 & 8\end{bmatrix}\overrightarrow y a. Find the eigenvalues and eigenvectors for the coeffi…

Question

Consider the linear system:


`\overrightarrow y'=\begin{bmatrix}-6 & -4 \\12 & 8\end{bmatrix}\overrightarrow y`


a. Find the eigenvalues and eigenvectors for the coefficient matrix.

b. For each eigenpair in the previous part, form a solution of
`\overrightarrow y' = A\overrightarrow y`. Use
`t` as the independent variable in your answers.

c. Does the set of solutions you found form a fundamental set (i.e., linearly independent set) of solutions?

Answer 1

a. If A is the coefficient matrix, solve det(A - λI) = 0 for the eigenvalues λ :

`\det\begin{bmatrix}-6-\lambda & -4 \\ 12 & 8-\lambda\end{bmatrix} = (-6-\lambda)(8-\lambda)+48 = 0 \implies \lambda(\lambda-2)=0`

`\implies \lambda = 0, \lambda = 2`

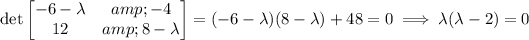
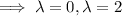
Let v = [v₁, v₂]ᵀ be the eigenvector corresponding to λ. Solve Av = λv for v :

`\lambda=0 \implies \begin{bmatrix}-6&-4\\12&8\end{bmatrix}\begin{bmatrix}v_1\\v_2\end{bmatrix} = \begin{bmatrix}0\\0\end{bmatrix} \implies 3v_1 + 2v_2 = 0`

If we pick v₂ = -3, then v₁ = 2, so [2, -3]ᵀ is the eigenvector for λ = 0.

`\lambda = 2 \implies \begin{bmatrix}-8&-4\\12&6\end{bmatrix}\begin{bmatrix}v_1\\v_2\end{bmatrix} = \begin{bmatrix}0\\0\end{bmatrix} \implies 2v_1 + v_2 = 0`

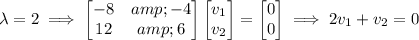
Let v₁ = 1, so v₂ = -2.

b. λ = 0 and v = [2, -3]ᵀ contributes a constant solution,

`\vec y_1 = e^(\lambda t) v = \begin{bmatrix}2\\-3\end{bmatrix}`

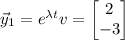
while λ = 2 and v = [1, -2]ᵀ contribute a solution of the form

`\vec y_2 = e^(\lambda t) v = e^(2t) \begin{bmatrix}1\\-2\end{bmatrix}`

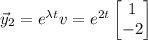
c. Yes; compute the Wronskian of the two fundamental solutions:

`W(1, e^(2t)) = \det\begin{bmatrix}1 & e^(2t) \\ 0 & 2e^(2t)\end{bmatrix} = 2e^(2t) \\eq 0`

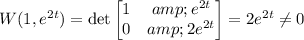
The Wronskian is non-zero, so the solutions are independent.