Answer:
m = 7/9
m = 7/9m ≈ 0.80
Explanation:
Given two points:
(16, 14), (-2, 0)
To find:
The slope
Solution:
We know that,
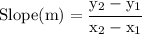
According to the question,
- y_2 = 0
- y_1 = 14
- x_2 = -2
- x_1 = 16
Note:[The underscore refers to that the numbers after the underscore is a subscript]
So Substitute them on the formulae:
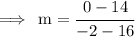
Simplify it.
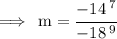
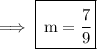
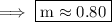
Thus,the slope is 7/9 in fraction and 0.80 (Nearest tenth) in decimal.