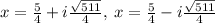Question

2x2 – 5x + 67 = 0

What would be your first step in completing the square for the equation above?

Answer 1

The first step is to divide all the terms by the coefficient of
`x^(2)` which is 2.

The solutions to the quadratic equation
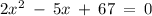`2x^2\:-\:5x\:+\:67\:=\:0` are:

`x=(5)/(4)+i(√(511))/(4),\:x=(5)/(4)-i(√(511))/(4)`

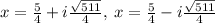
Explanation:

Considering the equation

`2x^2\:-\:5x\:+\:67\:=\:0`

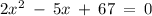
The first step is to divide all the terms by the coefficient of
`x^(2)` which is 2.

so

`(2x^2-5x)/(2)=(-67)/(2)`

`x^2-(5x)/(2)=-(67)/(2)`

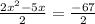
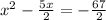
Lets now solve the equation by completeing the remaining steps

Write equation in the form:
`x^2+2ax+a^2=\left(x+a\right)^2`

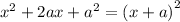
Solving for
`a`,

`2ax=-(5)/(2)x`

`a=-(5)/(4)`

`\mathrm{Add\:}a^2=\left(-(5)/(4)\right)^2\mathrm{\:to\:both\:sides}`

`x^2-(5x)/(2)+\left(-(5)/(4)\right)^2=-(67)/(2)+\left(-(5)/(4)\right)^2`

`x^2-(5x)/(2)+\left(-(5)/(4)\right)^2=-(511)/(16)`

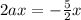
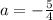
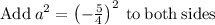
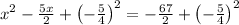
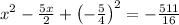
Completing the square

`\left(x-(5)/(4)\right)^2=-(511)/(16)`

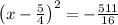
Since, you had required to know the first step in completing the square for the equation above, I hope you have got the point, but let me quickly solve the remaining solution.

For
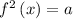`f^2\left(x\right)=a` the solution are
`f\left(x\right)=√(a),\:-√(a)`

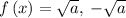
Solving

`x-(5)/(4)=\sqrt{-(511)/(16)}`

`x-(5)/(4)=√(-1)\sqrt{(511)/(16)}`

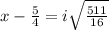`x-(5)/(4)=i\sqrt{(511)/(16)}` ∵ Applying imaginary number rule
`√(-1)=i`

`x-(5)/(4)=i(√(511))/(√(16))`

`-(5)/(4)=i(√(511))/(4)`

`x=(5)/(4)+i(√(511))/(4)`

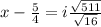
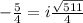
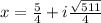
Similarly, solving

`x-(5)/(4)=-\sqrt{-(511)/(16)}`

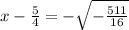
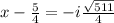`x-(5)/(4)=-i(√(511))/(4)` ∵ Applying imaginary number rule
`√(-1)=i`

`x=(5)/(4)-i(√(511))/(4)`

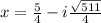
Therefore, the solutions to the quadratic equation are:

`x=(5)/(4)+i(√(511))/(4),\:x=(5)/(4)-i(√(511))/(4)`