Answer:
In assumption, x is the smaller even integer and x+2 is the next so it will be larger.
The integers are 4 and 6
Explanation:
Let the two consecutive even integers be x and x+2
Here x is the smaller even integer and x+2 is the next so it will be larger.
Now according to the given statement
Sum of both:
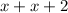
difference of 3 times the larger & 2 times the smaller:
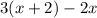
Putting the sum and difference equal:
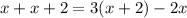
Solving the equation
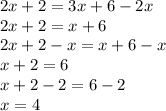
The next integer will be:
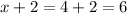
Hence,
In assumption, x is the smaller even integer and x+2 is the next so it will be larger.
The integers are 4 and 6.