Answer:
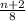 has a remainder of 7 ⇒ B
has a remainder of 7 ⇒ B
Explanation:
In m ÷ n = c +
 ,
,
Let us use the facts above to solve the question
∵
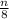 has a remainder of 5
has a remainder of 5
→ Let us find the first number divided by 8 and give a reminder of 5
that means let the quotient = 1
∵ n = (8 × 1) + 5 = 8 + 5
∴ n = 13
∵
 has a remainder of 7
has a remainder of 7
→ Let us find the first number divided by 8 and give a reminder of 7
that means let the quotient = 1
∵ n + x = (8 × 1) + 7 = 8 + 7
∴ n + x = 15
∵ n = 13
∴ 13 + x = 15
→ Subtract 13 from both sides
∴ 13 -13 + x = 15 - 13
∴ x = 2
∴
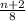 has a remainder of 7
has a remainder of 7