Question

Alandra's rectangular cake pan is 33\text{ cm}33 cm33, start text, space, c, m, end text by 23\text{ cm}23 cm23, start text, space, c, m, end text. She has enough batter to fill it to a depth of 3\text{ cm}3 cm3, start text, space, c, m, end text. Instead, Alandra wants to pour the batter into ice cream cones. She plans to fill each cone to a depth of 9\text{ cm}9 cm9, start text, space, c, m, end text with a diameter of 4\text{ cm}4 cm4, start text, space, c, m, end text.

Answer 1

By calculating the volumes of the batter and one cone, we find that Alandra can fill approximately 60 ice cream cones with her cake batter.

Step-by-step explanation:

The problem presented is a classic example of volume conversion from one shape to another, specifically from a rectangular prism (the cake pan) to cones (the ice cream cones). To determine how many cones Alandra can fill with her batter, we need to calculate the volume of the batter and the volume of each cone, then divide the total batter volume by the volume of one cone.

To calculate the volume of the batter, we use the formula for the volume of a rectangular prism which is length × width × height. Using the dimensions given, the volume of the batter that would fill the cake pan is:

Volume of the batter = 33 cm × 23 cm × 3 cm = 2277 cm³.

To calculate the volume of one cone, we use the formula for the volume of a cone which is (1/3)π(radius)^2(height). The diameter of the cone is given as 4cm, so the radius is 2 cm. Using the dimensions provided:

Volume of one cone = (1/3)π
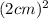`(2 cm)^2`(9 cm) ≈ (1/3)π
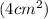`(4 cm^2)`(9 cm) ≈ 37.68 cm³ (approx).

Now we can find out how many cones Alandra can fill by dividing the volume of the batter by the volume of one cone:

Number of cones Alandra can fill = 2277 cm³ / 37.68 cm³ ≈ 60 cones (rounded down)

Alandra will be able to fill around 60 ice cream cones with her cake batter.