Answer:
The length of AB is
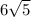 units
units
Explanation:
The rule of the distance between two points (x1, y1) and (x2, y2) is
∵ The endpoints of AB are (-4, 5) and (2, -7)
→ Let point (-4, 5) be (x1, y1) and point (2, -7) be (x2, y2)
∴ x1 = -4 and y1 = 5
∴ x2 = 2 and y2 = -7
→ Substitute them in the rule above to find the length of AB
∵
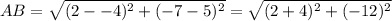
∴
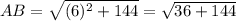
∴

∴ The length of AB is
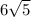 units
units