Question

The graph of an exponential function has a y-intercept of 8 and contains the point (3,64). Find the exponential function that describes the graph.

Answer 1

Answer: Do you have a picture

Explanation:

Answer 2

Given:

Y-intercept of exponential function is 8.

It contains the point (3,64).

To find:

The exponential function that describes the graph.

Solution:

The general form of an exponential function is

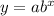`y=ab^x` ...(i)

where, a is initial value or y-intercept and b is growth factor.

Since, y-intercept is 8, therefore, a=8.

Put a=8 in (i).

`y=8b^x` ...(ii)

It contains the point (3,64). Put x=3 and y=64.

`64=8b^3`

Divide both sides by 8.

`(64)/(8)=b^3`

`8=b^3`

`2^3=b^3`

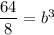
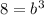
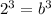
On comparing both sides, we get

`b=2`

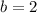
Put b=2 in (ii).

`y=8(2)^x`

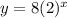
The functions form of this equation is

`f(x)=8(2)^x`

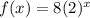
Therefore, the required function is
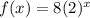`f(x)=8(2)^x`.