Question

Outside temperature over a day can be modeled as a sinusoidal function. Suppose you know the temperature varies between 73 and 97 degrees during the day and the average daily temperature first occurs at 10 AM. How many hours after midnight, to two decimal places, does the temperature first reach 82 degrees?

Answer 1

Answer: After about 9.03 hours the temperature first reach 82 degrees.

Explanation:

The sinusoidal function is given by :

`y=A\sin[\omega(x-\alpha)]+C`

where, A = amplitude;
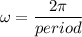`\omega=(2\pi)/(period)` , α= phase shift on the Y-axis and C = midline.

As per given,

Average daily temperature=
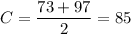`C=(73+97)/(2)=85` [midline is average of upper and lower limit.]

A= 97-85 = 12

Phase shift:
`\alpha=10`

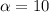
Period = 24 hours;

`\omega=(2\pi)/(24)=(\pi)/(12)`

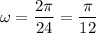
Substitute all values in sinusoidal function, we get

`y=12\sin[(\pi)/(12)(x-10)]+85`

Put y= 82, we get

`82=12\sin[(\pi)/(12)(x-10)]+85\\\\\Rightarrow\ -3= 12\sin[(\pi)/(12)(x-10)]\\\\=(-1)/(4)= \sin[(\pi)/(12)(x-10)]\\\\\Rightarrow\ (\pi)/(12)(x-10)=\sin^(-1)((-1)/(4))\\\\\Rightarrow\ x-10=(12)/(\pi)(\sin^(-1)((-1)/(4)))\\\\\Rightarrow\ x=(12)/(\pi)(\sin^(-1)((-1)/(4)))+10\\\Rightarrow\ x\approx9.03`

Hence, After about 9.03 hours the temperature first reach 82 degrees.