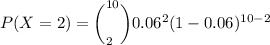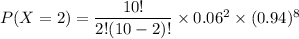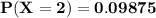Question

Twenty percent of all telephones of a certain type are submitted for service while under warranty. Of these, 70% can be repaired, whereas the other 30% must be replaced with new units. If a company purchases ten of these telephones, what is the probability that exactly two will end up being replaced under warranty?

Answer 1

The required probability is 0.09875

Explanation:

From the given information;

the probability of repairing the telephones = 0.70

the probability of the replaced = 0.30

Suppose we consider Mto denotes the telephone that is submitted for service while under warranty and must be replaced.

Then;

p = P(S) = P(replaced | submitted) P(submitted)

= 0.30 × 0.20

= 0.06

Now, the probability that exactly two will end up being replaced under warranty given that it assumes a binomial distribution where n = 10 and p = 0.06

`P(X=2)=\bigg (^(10)_(2)\bigg) 0.06^2(1-0.06)^(10-2)`

`P(X=2)=(10!)/(2!(10-2)!)* 0.06^2* (0.94)^(8)`

`\mathbf{P(X=2)=0.09875}`