Answer:
5.199
Explanation:
From the information provided;
We know that λ = 0.5.
However, the control limits for a steady-state EMWA control chart is:
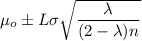
where;
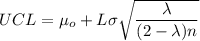
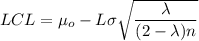
Given that the data is chosen from an individual sample;
Then; we can express the width as:
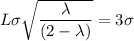
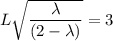
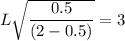
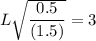
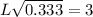
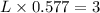
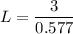
L = 5.199