Question

An EWMA control chart uses λ = 0.5. What is the value of L such that the control limits of this EWMA control chart in the steady state have the same width with a 3σ X_bar control chart?

Answer 1

5.199

Explanation:

From the information provided;

We know that λ = 0.5.

However, the control limits for a steady-state EMWA control chart is:

`\mu_o \pm L \sigma \sqrt{(\lambda )/((2-\lambda )n)}`

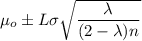
where;

`UCL = \mu_o + L \sigma \sqrt{(\lambda )/((2-\lambda )n)}`

`LCL = \mu_o- L \sigma \sqrt{(\lambda )/((2-\lambda )n)}`

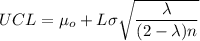
Given that the data is chosen from an individual sample;

Then; we can express the width as:

`L \sigma \sqrt{(\lambda)/((2-\lambda))}= 3 \sigma`

`L \sqrt{(\lambda)/((2-\lambda))}= 3`

`L \sqrt{(0.5)/((2-0.5))}= 3`

`L \sqrt{(0.5)/((1.5))}= 3`

`L √(0.333)= 3`

`L* 0.577= 3`

`L=( 3 )/(0.577)`

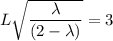
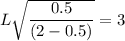
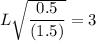
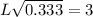
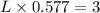
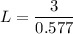
L = 5.199