Question

An automotive fuel cell consumes fuel at a rate of 28m3/h and delivers 80kW of power to the wheels. If the hydrogen fuel has a heating value of 141,790 kJ/kg and a density of 0.0899 kg/m3, determine the efficiency of this fuel cell.

Answer 1

The efficiency of this fuel cell is 80.69 percent.

Step-by-step explanation:

From Physics we define the efficiency of the automotive fuel cell (
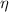`\eta`), dimensionless, as:

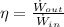`\eta = (\dot W_(out))/(\dot W_(in))` (Eq. 1)

Where:

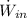`\dot W_(in)` - Maximum power possible from hydrogen flow, measured in kilowatts.

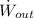`\dot W_(out)` - Output power of the automotive fuel cell, measured in kilowatts.

The maximum power possible from hydrogen flow is:

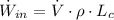`\dot W_(in) = \dot V\cdot \rho \cdot L_(c)` (Eq. 2)

Where:

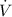`\dot V` - Volume flow rate, measured in cubic meters per second.

`\rho` - Density of hydrogen, measured in kilograms per cubic meter.

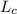`L_(c)` - Heating value of hydrogen, measured in kilojoules per kilogram.

If we know that
`\dot V = (28)/(3600)\,(m^(3))/(s)`,
`\rho = 0.0899\,(kg)/(m^(3))`,
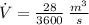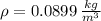`L_(c) = 141790\,(kJ)/(kg)` and
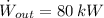`\dot W_(out) = 80\,kW`, then the efficiency of this fuel cell is:

(Eq. 1)

`\dot W_(in) = \left((28)/(3600)\,(m^(3))/(s)\right)\cdot \left(0.0899\,(kg)/(m^(3)) \right)\cdot \left(141790\,(kJ)/(kg) \right)`

`\dot W_(in) = 99.143\,kW`

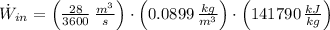
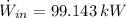
(Eq. 2)

`\eta = (80\,kW)/(99.143\,kW)`

`\eta = 0.807`

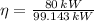
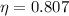
The efficiency of this fuel cell is 80.69 percent.