Answer:
width = 10 m
length = 16 m
Explanation:
Formula

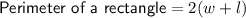
(where
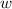 is width and
is width and
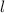 is length)
is length)
Given:
- Area = 160 m²
- Perimeter = 52 m
Substituting the given values into the formulae to create two equations:

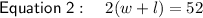
Rearranging Equation 1 to make w the subject:
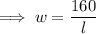
Substituting expression for w into Equation 2 and solving for
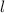 :
:
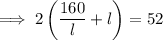
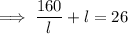
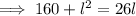

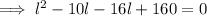
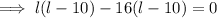
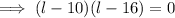

According to Equation 1:
- If length = 10 m ⇒ width = 16 m
- If length = 16 m ⇒ width = 10 m
As width < length, the dimensions of the shop are:
- width = 10 m
- length = 16 m