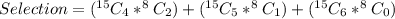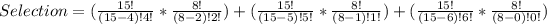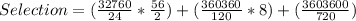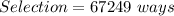Question

Suppose that a department contains 8 men and 15 women. How many ways are there to form a committee with six members if it must have more women than men?

Answer 1

`Selection = 67249\ ways`

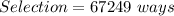
Explanation:

Given

`Men = 8`

`Women = 15`

`Committee = 6`

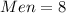
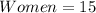
Required

Determine the number of selections if the committee must have more women

To have more women, the selection has to be:

(4 women and 2 men) or (5 women and 1 man) or (6 women and 0 man)

Where each selection is calculated using:

`^nC_r = (n!)/((n - r)!r!)`

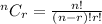
So, the selection is calculated as thus:

`Selection = (^(15)C_4 * ^(8)C_2) + (^(15)C_5 * ^(8)C_1) + (^(15)C_6 * ^(8)C_0)`

`Selection = ((15!)/((15 - 4)!4!) * (8!)/((8 - 2)!2!)) + ((15!)/((15 - 5)!5!) * (8!)/((8 - 1)!1!)) + ((15!)/((15 - 6)!6!) * (8!)/((8 - 0)!0!))`

`Selection = ((15!)/(11!4!) * (8!)/(6!2!)) + ((15!)/(10!5!) * (8!)/(7!1!)) + ((15!)/(9!6!) * (8!)/(8!0!))`

`Selection = ((15 * 14 * 13 * 12)/(4 * 3 * 2 * 1) * (8 * 7)/(2 * 1)) + ((15 * 14 * 13 * 12 * 11)/(5*4*3*2*1) * (8)/(1)) + ((15 * 14 * 13 * 12 * 11 * 10)/(6*5*4*3*2*1) * (1)/(1))`

`Selection = ((32760)/(24) * (56)/(2)) + ((360360)/(120) * 8) + ((3603600)/(720))`

`Selection = (1365 * 28) + (3003 * 8) + (5005)`

`Selection = 38220 + 24024 + 5005`

`Selection = 67249\ ways`