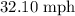Question

At noon, ship A is 40 miles due west of ship B. Ship A is sailing west at 24 mph and ship B is sailing north at 22 mph. How fast (in mph) is the distance between the ships changing at 4 PM? (Note: 1 knot is a speed of 1 nautical mile per hour.)

Answer 1

`32.10\ \text{mph}`

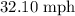
Explanation:

Distance traveled by A in 4 hours =
`24* 4=96\ \text{mi}=a`

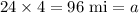
Distance traveled by B in 4 hours =
`22* 4=88\ \text{mi}=b`

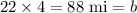
Total distance between A and the initial point of B is
`40+96=136\ \text{mi}`

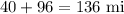
Distance between A and B 4 hours later

`c=√(136^2+88^2)\ \text{mi}`

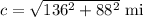
From Pythagoras theorem we have

`(a+40)^2+b^2=c^2`

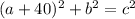
Differentiating with respect to time we get

`2(a+40)(da)/(dt)+2b(db)/(dt)=2c(dc)/(dt)\\\Rightarrow (a+40)(da)/(dt)+b(db)/(dt)=c(dc)/(dt)\\\Rightarrow (dc)/(dt)=((a+40)(da)/(dt)+b(db)/(dt))/(c)\\\Rightarrow (dc)/(dt)=((96+40)*24+88* 22)/(√(136^2+88^2))\\\Rightarrow (dc)/(dt)=32.10\ \text{mph}`

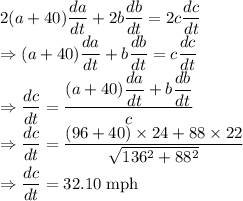
So, the the distance between the ships at 4 PM is changing at
`32.10\ \text{mph}`