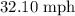Answer:
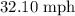
Explanation:
Distance traveled by A in 4 hours =
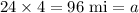
Distance traveled by B in 4 hours =
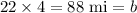
Total distance between A and the initial point of B is
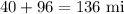
Distance between A and B 4 hours later
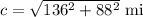
From Pythagoras theorem we have
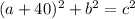
Differentiating with respect to time we get
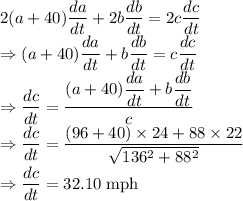
So, the the distance between the ships at 4 PM is changing at