Question

A directed segment ¯¯¯¯¯¯¯ S T is partitioned from S ( − 5 , 0 ) to T ( 20 , 25 ) in a 3 2 ratio at point M . What are the coordinates of M ? ( − 15 , − 10 ) ( − 15 , − 10 ) ( 5 , 15 ) ( 5 , 15 ) ( 10 , 15 ) ( 10 , 15 ) ( 15 , 5 ) ( 15 , 5 )

Answer 1

Answer:Find the distance between the given points: (-7, 5) and (-8, 4)

Find the distance between the given points: (-7, 5) and (-8, 4)

Step-by-step explanation:

Find the distance between the given points: (-7, 5) and (-8, 4)

Answer 2

( 10 , 15 )

Step-by-step explanation:

If two points
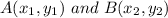`A(x_1,y_1)\ and\ B(x_2,y_2)` form a line segment AB and is divided in the ratio of m:n by a point O(x, y). The coordinates of point O is calculated as follows:

`x=(n)/(n+m)(x_2-x_1) +x_1\\\\y=(n)/(n+m)(y_2-y_1) +y_1`

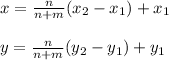
Given Segment ST from S(−5 , 0 ) to T(20, 25 ) divided in a 3:2 ratio by point M. Let us assume the coordinates of M is at (x, y), then:

`x=(3)/(3+2)(20-(-5)) +(-5)\\\\x=(3)/(5)(25)-5=15-5\\\\x=10 \\\\y=(3)/(3+2)(25-0)+0\\\\y=(3)/(5) (25)\\\\y=15`

The coordinate of M is at (10, 15)