Answer:
Standard form = (x + 5)² + y² = 117
General Form = x² + 10x + y² - 92 = 0
Step-by-step explanation:
(x - h)² + (y - k)² = r²
Find radius using:
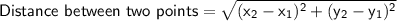

Find equation inserting values: Given center: (-5, 0)
⇒ (x - (-5))² + (y - 0)² = (3√13)²
⇒ (x + 5)² + y² = 117
⇒ x² + 10x + 25 + y² - 117 = 0
⇒ x² + 10x + y² - 92 = 0