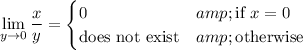Neither of these statements are true.
x/∞ = 0 is a nonsensical statement. It's more accurate to say

for any real number x. The important bit is that y is an arbitrarily large number as it approaches ∞. To convince yourself that this expression approaches 0 as y gets larger and larger, try fixing x and pick any increasing sequence of numbers for y.
For example, let x = 1 and take y from the sequence of increasing powers of 10, {10, 10², 10³, …}, which grows without bound. Then
1/10 = 0.1
1/10² = 0.01
1/10³ = 0.001
and so on. Naturally, the larger the power of 10 and thus the larger y gets, the closer x/y gets to 0.
Similarly, x/0 is nonsense, but the "limit-ized" version of the claim is also incorrect. For any fixed real number x, the limit
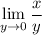
does not exist. Suppose x > 0. If y approaches 0 from above, then y > 0 and x/y > 0 and
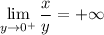
which you can convince yourself is true by reversing the example from before. Let x = 1 and take y from the sequence of decreasing powers of 10, {1/10, 1/10², 1/10³, …}, which converges to 0. Then
1/(1/10) = 10
1/(1/10²) = 100
1/(1/10³) = 1000
and so on. The smaller y gets (while still being positive), the larger x/y becomes.
But now suppose y < 0 and that y approaches 0 from below. Then x/y < 0, and
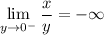
The limits from either side do not match, so the limit as y approaches 0 does not exist.
You can use the same reasoning for when x < 0.
The case of x = 0 is special, however. Since y is approaching 0, it's never actually the case that y = 0. 1/y is then some non-zero real number, and multiplying it by x = 0 makes x/y = 0. Then
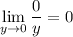
So in general,